中心極限定理
中心極限定理は、「母集団の分布の形状によらず、そこから抽出した標本の平均値は正規分布に従う。」という定理です。平均値算出時のデータ数(標本サイズ)は、大きいほど正規分布に従います。
母集団が、平均μ、分散σ^2の確率分布に従う場合、標本平均の分布は、平均μ、分散σ^2/nの正規分布に近づきます。
具体例
例えばここに歪んだコインがあるとします。表が出る確率が30%、裏が出る確率が70%です。
表が出ることを「1」、裏が出ることを「0」と表すと、以下のような確率分布となります。
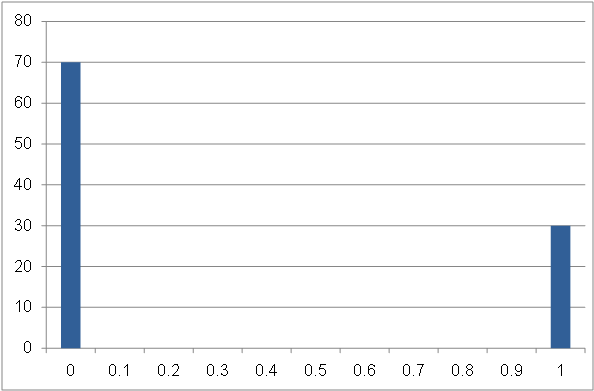
このコインをn回投げた時の平均値について、何度も何度も確認します。
例えばn=10とした場合は、コインを10回投げた平均値を求めます。その結果が、0、0、1、0、1、1、0、0、0、0 であれば、平均値は0.3です。これを何度も行います。
そうすると、次のようなヒストグラムが出来上がります。(なお、平均値算出を行った回数は関係ないので、縦軸は消しています。)
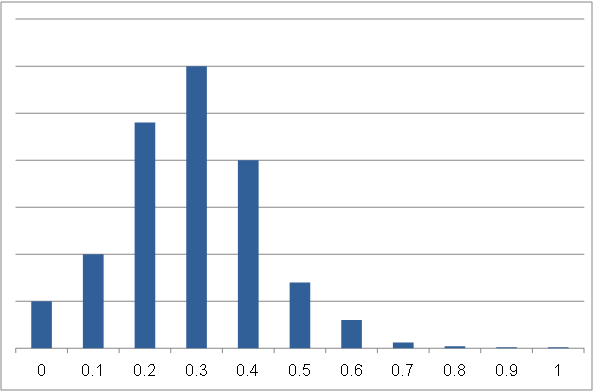
1(=表)が出る確率が30%なので、平均値0.3の回数が多くなります。
そしてこのヒストグラムの形は、正規分布に近いことが分かると思います。
中心極限定理はこのように、平均値の分布が正規分布に従うという定理です。
つまり、何かしらの平均値は、正規分布から抽出された値とみなせるわけです。
一般的には、nの数(標本サイズ)は30もあれば、平均値は正規分布に従っているとみなせますが、もともとの分布が歪んでいる場合は、より多くの数が必要になるとされています。
今回は一例として、もともとの分布を2値の確率分布としましたが、そうでなくても成り立つ法則です。
メリット
中心極限定理により、もともとの分布の形状を知らなくても、正規分布を利用したデータ解析が可能になります。
正規分布は統計の基礎となる分布で、t検定や信頼区間の算出など、多くのシーンで正規分布を仮定していますので、それらが利用できる点は、大きなメリットです。
まとめ
中心極限定理は、「母集団の分布の形状によらず、そこから抽出した標本の平均値は正規分布に従う。」という定理です。
これにより、もともとの分布の形状を知らなくても、正規分布を利用したデータ解析が可能になります。

