箱ひげ図
箱ひげ図は、データの散らばりを視覚的に把握するための図です。
その名の通り、箱(四角形)と、ひげ(直線)から成ります。
データの散らばりは、分散、標準偏差、四分位数などで表されますが、箱ひげ図は、四分位数の散らばりを視覚化します。
四分位数が分からない場合は、以下のページを参考にしてください。
箱ひげ図が示すもの
箱ひげ図は、次のものを示します。
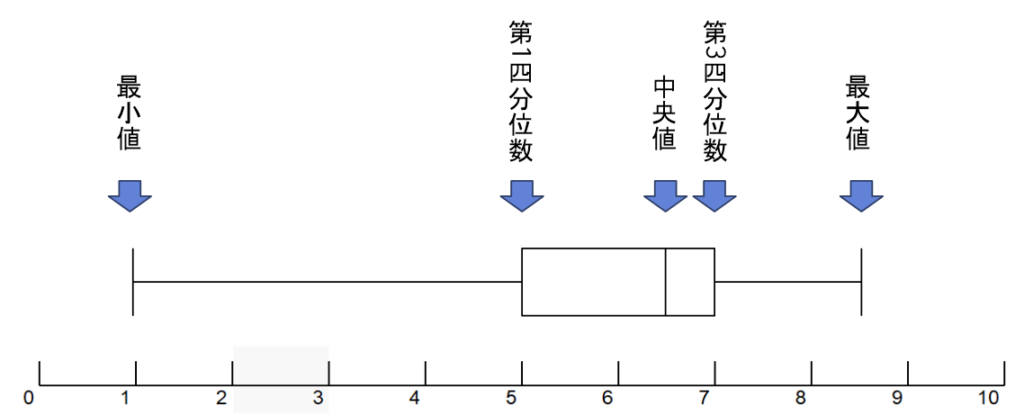
・最小値、最大値
・第1四分位数、中央値、第3四分位数
・外れ値
こちらが基本の形になります。
また、箱ひげ図にはいくつかの書き方がありますが、外れ値を示す箱ひげ図もよく利用されます。
次の図の「〇」が外れ値です。
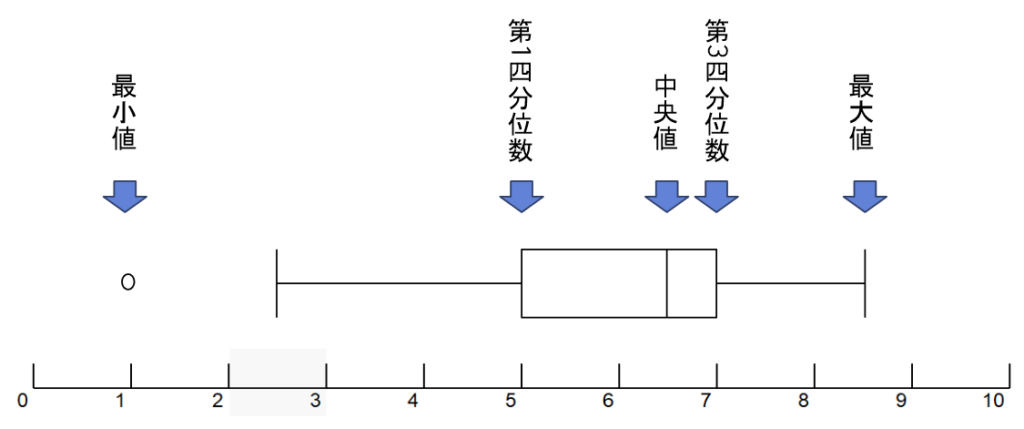
外れ値を示す場合の箱ひげ図は、次のようにして作図されます。
ひげの長さの決め方(下端)
まず、四分位範囲の1.5倍を求めます((7-5)×1.5=3)。求めた値の分だけ第1四分位数から下の範囲を確認し、その範囲(5~2)で一番小さいデータをひげの下端とします。
ひげの長さの決め方(上端)
まず、四分位範囲の1.5倍を求めます((7-5)×1.5=3)。求めた値の分だけ第3四分位数から上の範囲を確認し、その範囲(7~10)で一番大きいデータをひげの上端とします。
下端と上端より外にあるデータは、外れ値として、全て「〇」で表されます。
箱ひげ図のイメージ
ここからは、箱ひげ図のイメージを掴むための説明です。
最後に注意書きをしていますが、あくまでもイメージのための話です。
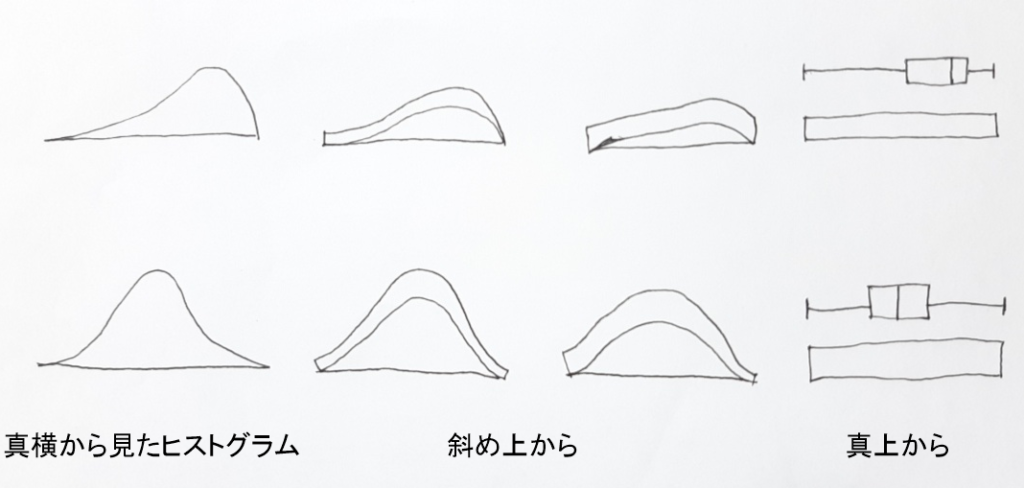
一番左は、真横からヒストグラムとします。ここから見る角度を徐々に上へと移動し、ヒストグラムを上から覗いた図が、箱ひげ図となります。
四分位数の定義より、最小値から第1四分位数、第1四分位数から中央値、中央値から第3四分位数、第3四分位数から最大値のデータの個数は同じです。
データの数が同じなのに、間隔が狭いということは、頻度が急激に上がっている(または下がっている)ことを意味し、逆に、間隔が広いということは、ゆるやかに変化していることを意味します。
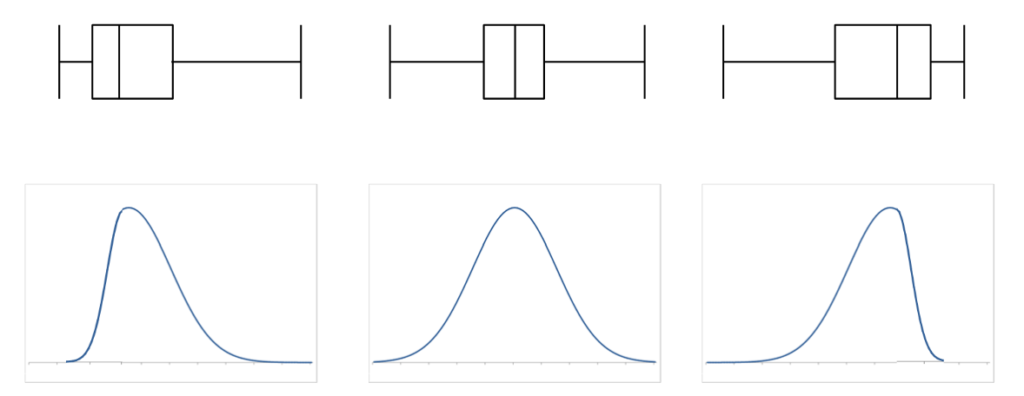
また、次の図からは、箱ひげ図が散らばりを表現するという事が伝わりやすいと思います。
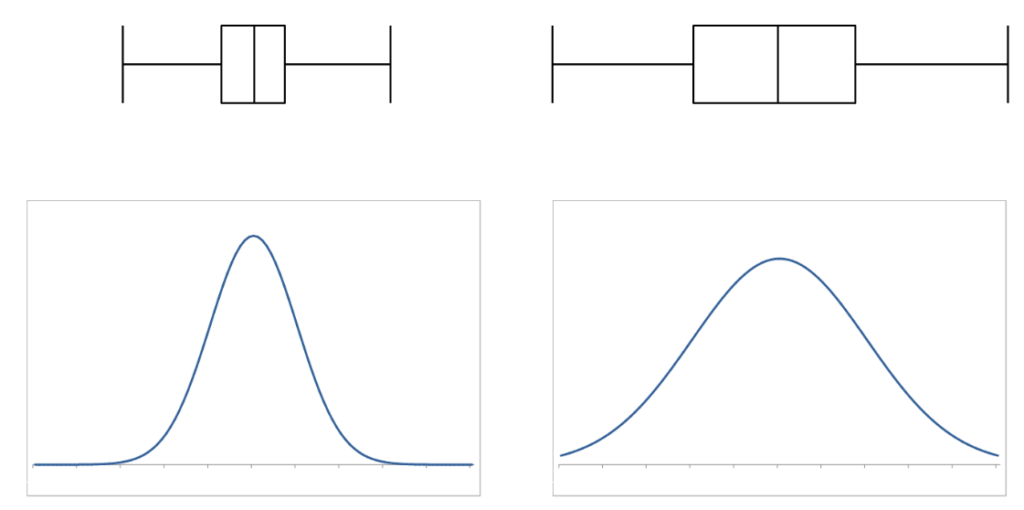
【注意】
箱ひげ図は、必ずしも山が1つの分布を表しているとは限りません。山が2つ以上の分布を表していることもあります。
ただ、箱ひげ図は、山が1つの分布を表すときに有効であり、2つ以上の特殊な分布では、十分な情報の集約ができないため、イメージとして1つ山を使うのは間違っていないと思います。
まとめ
箱ひげ図は、四分位数を使って、データの散らばりを視覚的に把握するための図です。
最大値、最小値、第1四分位数、中央値、第3四分位数、(必要に応じて)外れ値が示されます。


